Analysis on 'Third Maximum Number' Problem in Depth

In Leetcode, you can find the problem: Third Maximum Number. I will dive into the solution right away assuming that you have already solved (or at least tackled) the problem.

1. Limit the size of priority queue

Although this solution may look simple and good, it takes extra time.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
 
class Solution {
public:
    int thirdMax(vector<int>& nums) {
        priority_queue<int> pq;
        unordered_set<int> distNumSet;

        for (int n: nums) {
            if (distNumSet.find(n) == distNumSet.end()) {
                distNumSet.insert(n);
                pq.push(n);
            }
        }
        if (pq.size() >= 3) {
            pq.pop();
            pq.pop();
        }
        return pq.top();
    }
};
 

Why is that? Let’s look at the second solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
 
class Solution {
public:
    int thirdMax(vector<int>& nums) {
        priority_queue<int, vector<int>, greater<int>> pq;
        unordered_set<int> distNumSet;

        for (int n: nums) {
            if (distNumSet.find(n) == distNumSet.end()) {
                distNumSet.insert(n);
                pq.push(n);
            }
            if (pq.size() > 3) {
                pq.pop();
            }
        }
        if (pq.size() == 2) {
            pq.pop();
        }
        return pq.top();
    }
};
 

The second solution always maintains the size of priority queue to three, making the time complexity of push operation to O(1) (at most log3). On the other hand the first solution inserts every distinct element in nums into the priority queue. This will cause push operation to take O(logn) time.

But I wasn’t still satisfied. It still gives 7 ms of runtime. In Leetcode, well-optimized C++ code submission usually returns 0 ms.

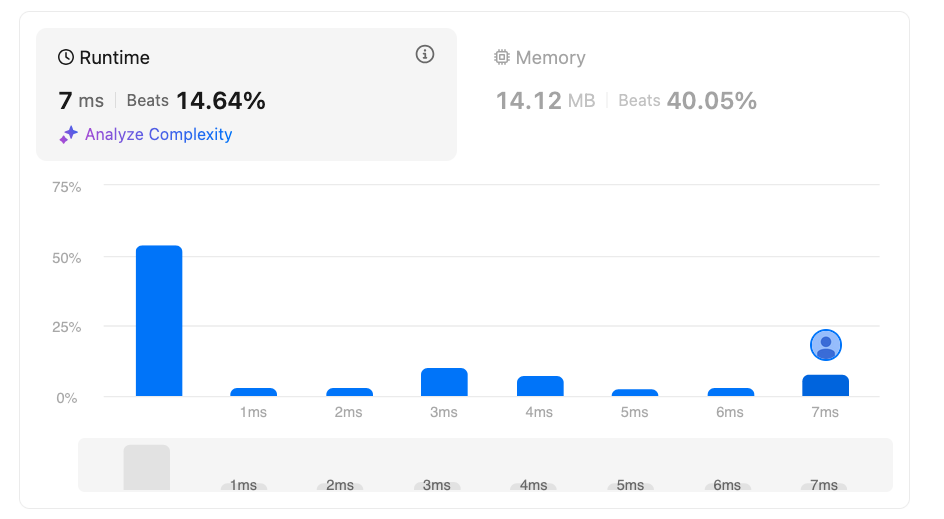
How can we make even faster?

2. Third Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
 
class Solution {
public:
    int thirdMax(vector<int>& nums) {
        priority_queue<int, vector<int>, greater<int>> pq;
        unordered_set<int> distNumSet;

        for (int n: nums) {
            if (distNumSet.find(n) == distNumSet.end()) {
                if (pq.size() == 3 && n > pq.top()) {
                    distNumSet.erase(pq.top());
                    pq.pop();
                    pq.push(n);
                    distNumSet.insert(n);
                }
                else if (pq.size() < 3) {
                    pq.push(n);
                    distNumSet.insert(n);
                }
            }
            if (pq.size() > 3) {
                pq.pop();
            }
        }
        if (pq.size() == 2) {
            pq.pop();
        }
        return pq.top();
    }
};
 

This code has some more improvements:

• It removes an element from set if the element is smaller than the current num n
  • In this way, it reduces the size of the set. In C++, set find method takes average time of O(1) but in worst case it takes O(n).
• It compares the current number n and the minimum number in pq (pq.top()) first, and then decides to run push or pop operation. This prevents unnecessary execution of push operation in some cases.
  • In the previous solution, it ran push operation no matter what the current number n was and then it popped an element from pq. The code looks simpler in this way, but it may take more time if the size of pq is much greater.

3. Intersting fact: index-based iteration in C++ does make difference

If you change a line in the third solution:

1
2
3
4
5
6
7
8
 
class Solution {
public:
    int thirdMax(vector<int>& nums) {
		// ...

        // for (int n: nums) {
        for (int i = 0; i < nums.size(); i++) {
        // ...
 

It will improve the runtime complexity from 3 ms to 0 ms. Why does it make such big difference?

1. Compiler Optimization

Index-based loops are often easier for compilers to optimize. In this case, the compiler might be able to apply more aggressive optimizations to the index-based loop, such as:

• Loop unrolling
• Vectorization
• Better instruction pipelining

These optimizations can lead to significant performance improvements, especially for large arrays.

2. Memory Access Patterns

Index-based loops can sometimes result in more cache-friendly memory access patterns. When iterating over a vector using indices, the memory accesses are typically more predictable and sequential, which can lead to better cache utilization.

3. Iterator Overhead

Range-based for loops use iterators internally. While modern compilers are generally good at optimizing these, there can still be some overhead associated with iterator creation and manipulation, especially for complex container types.

4. Inlining and Function Call Elimination

Index-based loops may allow the compiler to more easily inline and eliminate function calls. This can reduce function call overhead and allow for more aggressive optimizations across loop iterations.

5. Bounds Checking

Some implementations of range-based for loops may include additional bounds checking that isn’t as easily optimized away as with index-based loops.